北京市考行测数量关系,统筹出最短时间
北京市考行测技巧
在行测考试中,统筹问题中的时间优化问题是一类常考题型,时间优化即研究如何合理地使用人力物力才能够保证完成一项工作时所花的时间最少。这类问题包含排队取水、烙饼问题、过桥问题等等,其中最常考查的就是排队取水问题,今天小编带大家一起来了解一下这类题目的解题技巧:
数量关系例题讲解
题型特征
多个人排队取水,已知每个人取水的时间且各不相同,一个一个进行,计算排队等待和取水时间总和的最小值是多少。
例题、有甲、乙、丙三位同学每人拿一只桶同时到一个公用的水龙头灌水,灌水所需的时间分别为1.5分钟、0.5分钟和1分钟。若只能逐个地灌水,未轮到的同学需等待,灌完的同学立即离开,那么这三位同学花费的时间(包括等待时间)的总和最少是几分钟?
A.3分钟
B.5分钟
C.5.5分钟
D.7分钟
【解析】最终要求的总时间应该是由灌水时间和排队等待的时间组成的,而其中三个人灌水所花的时间是固定的,那我们要让总时间最少,就得让三位同学等待的时间尽可能地短。之所以会产生等待的时间,是因为我们只有一个水龙头,就意味着第一个人在灌水的时候,另外两个人是需要等待的,所以我们要让等待的时间尽可能地短就要研究一下三位同学灌水的顺序:
如果第一个灌水的是甲同学,他灌水需要1.5分钟,那就意味着乙、丙同学分别都要等待1.5分钟;如果第一个灌水的是乙同学,他灌水需要0.5分钟,就说明剩下的甲、丙两位同学分别都要等待0.5分钟;如果第一个灌水的是丙同学,他灌水需要1分钟,就意味着甲和乙分别要等待1分钟。
对比这三种情况我们会发现第一个灌水的是乙同学就可以保证另外两个人等待的时间最短,也就说明我们解决排队取水问题的原则就是:让取水时间短的优先取水,即谁花的时间短谁先来。
因此三个人排队灌水的顺序应该是乙、丙、甲,具体灌水和等待的时间如下表所示:
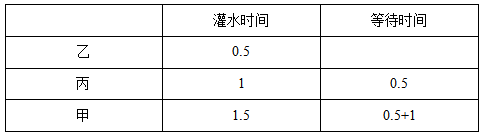
通过观察上表会发现0.5出现了三次,1出现了两次,1.5出现了一次,所以时间总和最短为0.5+1+0.5+1.5+0.5+1=5分钟,故本题选B。
总结:排队取水问题的解题原则为:让取水时间短的优先取水。
【思考】如果在上面例题的基础上,我们稍微增加一些条件,把题干中的“甲乙丙”三位同学变成“甲乙丙丁戊己庚”六位同学,已知他们灌水所需的时间分别为1.5分钟、0.5分钟、1分钟、2分钟、3分钟和5分钟,六人同时到一个公用的水龙头灌水,这样花费的时间总和最少是多少呢?
题目辨析:根据解题原则,我们可以首先确定这六位同学的打水顺序为乙、丙、甲、戊、己、庚,具体灌水和等待的时间如下表所示:
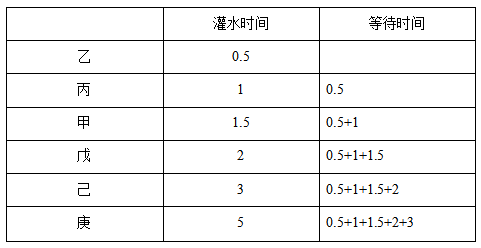
通过观察上表我们会发现每一个灌水时间都多次出现,那我们可以汇总一下:0.5出现了六次,1出现了五次,1.5出现了四次,2出现了三次,3出现了两次,5出现了一次,所以时间总和最少为0.5×6+1×5+1.5×4+2×3+3×2+5×1=31分钟。
总结:上面两道题目最终的算式中都涉及到了所有人的打水时间,解决排队取水问题可以分成两步走:第一步,按照打水所需时间将时间从大到小依次排开;第二步,按照从1开始的自然数与排好的顺序依次相乘。
小编相信通过今天的讲解,大家对于排队取水问题已经有了一定的了解,大家能够在复习的过程中再找几道题目巩固一下,这样在考试中出现此类问题时就能够快速求解。
北京市考行测资料查看
点击查看:北京公务员考试行测言语理解网络信息
点击查看:北京公务员考试行测数量关系网络信息
点击查看:北京公务员考试行测判断推理网络信息
点击查看:北京公务员考试行测资料分析网络信息
更多北京市考行测技巧与方法扫码获取
还想了解更多北京市考行测技巧?扫码回复“咨询老师”



扫码关注回复“咨询老师”



点击分享此信息:
 相关文章
相关文章


